今天开始安排了几节算法课程给孩子们。
算法五个特征:
有穷性: 一个算法应包括有限的运算步骤,执行了有穷的操作后将终止运算,不能是个死循环
确切性: 算法的每一步骤必须有确切的定义,读者理解时不会产生二义性。并且,在任何条件下,算法只有唯一的一条执行路径,对于相同的输入只能得出相同的输出
输入:一个算法有0个或多个输入,以描述运算对象的初始情况,所谓0个输入是指算法本身定义了初始条件
输出:一个算法有一个或多个输出,以反映对输入数据加工后的结果,这是算法设计的目的
可行性: 算法中每一步运算应该是可行的。算法原则上能够精确地运行,而且人能用笔和纸做有限次运算后即可完成
如何来评价一个算法的好坏呢?主要是从两个方面:
一是看算法运行所占用的时间,叫时间复杂度
二是看算法运行时所占用的空间,叫空间复杂度
1、求n!(n>1)
算法分析:n!表示n的阶乘,也就是
n!=n(n-1)(n-2)…1
参考代码
#include<iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int result = 1;
for(int i=1; i<=n; i++){
result *= i;
}
cout << result << endl;
return 0;
}2、求1-n的和。(n>1)
算法分析:total = 1+2+3+….+n
代码参考:
#include<iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int result = 0;
for(int i=1; i<=n; i++){
result += i;
}
cout << result << endl;
return 0;
}3、求n!阶乘累积之和。(n>1)
算法分析:n!表示n的阶乘
n!=n(n-1)(n-2)…1。累积之和也就是 n!+(n-1)!+(n-2)!+…+1
参考代码:
#include<iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int m = 0;//求和的
for(int k = 1; k <= n; k++){
int j = 1;//阶乘的
for(int i=1; i<=k; i++){
j *= i; //=> j = j * i;
}
//cout << j << endl;
m += j;
}
cout << m << endl;
return 0;
}4、汉诺塔问题讲解递归算法
如果一个对象的描述中包含它本身,我们就称这个对象是递归的,这种用递归来描述的算法称为递归算法。
递归算法存在的两个必要条件:
a. 必须有递归的终止条件;
b. 过程的描述中包含它本身
大家熟知的一个的故事:
从前有座山,山上有座庙,庙里有个老和尚在给小和尚讲故事,他说从前有座山,山上有座庙,庙里有个老和尚在给小和尚讲故事,他说……
#include<iostream>
using namespace std;
//讲故事-声明
void jiangushi(int cs);
int main()
{
jiangushi(1);
return 0;
}
//讲故事-实现
void jiangushi(int cs)
{
cout << cs << "次>>>" << "从前有座山,山上有座庙,庙里有个老和尚在给小和尚讲故事,他说从前有座山,山上有座庙,庙里有个老和尚在给小和尚讲故事,他说:" << endl;
if(cs == 10){
return;
}
cs++;
jiangushi(cs);
}汉诺塔问题,如下图,有A、B、C三根柱子。A柱子上按从小到大的顺序堆放了N个盘子,现在要把全部盘子从A柱移动到C柱,移动过程中可以借助B柱。移动时有如下要求:
(1)一次只能移动一个盘子;
(2)不允许把大盘放在小盘上边;
(3)盘子只能放在三根柱子上;
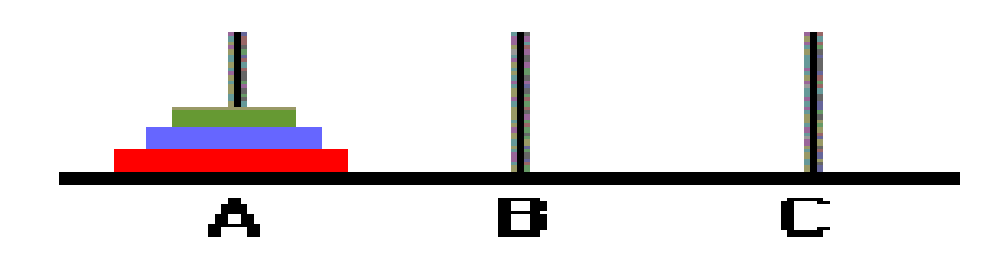
算法分析:
当盘子比较多的时,问题比较复杂,所以我们先分析简单的情况:
如果只有一个盘子,只需一步,直接把它从A柱移动到C柱;
如果是二个盘子,共需要移动3步:
(1)把A柱上的小盘子移动到B柱;
(2)把A柱上的大盘子移动到C柱;
(3)把B柱上的大盘子移动到C柱;
如果N比较大时,需要很多步才能完成,我们先考虑是否能把复杂的移动过程转化为简单的移动过程,如果要把A柱上最大的盘子移动到C柱上去,必须先把上面的N-1个盘子从A柱移动到B柱上暂存,按这种思路,就可以把N个盘子的移动过程分作3大步:
(1)把A柱上面的N-1个盘子移动到B柱;
(2)把A柱上剩下的一个盘子移动到C柱;
(3)把B柱上面的N-1个盘子移动到C柱;
其中N-1个盘子的移动过程又可按同样的方法分为三大步,这样就把移动过程转化为一个递归的过程,直到最后只剩下一个盘子,按照移动一个盘子的方法移动,递归结束。
#include<iostream>
using namespace std;
int step = 0;
void move(int n, char from, char to);
void hanoi(int n, char a, char b, char c);
int main()
{
int num;
while(1){
cout << "请输入盘子数量:";
cin >> num;
if(num < 1){
cout << "退出程序" << endl;
break;
}
step = 0;
hanoi(num, 'A', 'B', 'C');
cout << "需要:" << step << endl;
}
return 0;
}
void move(int n, char from, char to){
step ++;
cout << "第" << step << "步: 将" << n << "号盘子从" << from << "->" << to << endl;
}
void hanoi(int n, char a, char b, char c){
if(n == 1){
move(1, a, c);
}else{
hanoi(n-1, a, c, b);
move(n, a, c);
hanoi(n-1, b, a, c);
}
}
