三点估算(可用于进度管理和成本管理)
1、 期望(成本)时间—–通过计算得到,我们期望的一个工期T1
2、 悲观(成本)时间—–题目给出,最糟糕的情况T2
3、 乐观(成本)时间—–题目给出,最好的情况T3
4、 最可能(成本)时间—-题目给出,一般的情况T4
计算公式:
ß分布
期望工期 T1=(T2+T3+4*T4)/6
标准差(δ)=(悲观时间-乐观时间)/6
方差=δ²(标准差的平方)
三角分布(不常用)
T1=(T2+T3+T4)/3
进度估算

成本估算

算完工概率要知道三个数字:
1个标准差 68.3%
2个标准差 95.5%
3个标准差 99.7%
6个标准差 99.99%
例题
一个活动的最悲观估算为36天,最可能估算为21天,最乐观估算为6天。1)该活动在16至26天内完工的概率是?2)在第26天完工的概率为?
1)A. 99.73% B. 95.46% C. 84.24% D.68.26%
解题:均值 Te= (36+4∗21+6 )/6 = 21天
标准差 𝛿 = (36−6) /6 = 5天
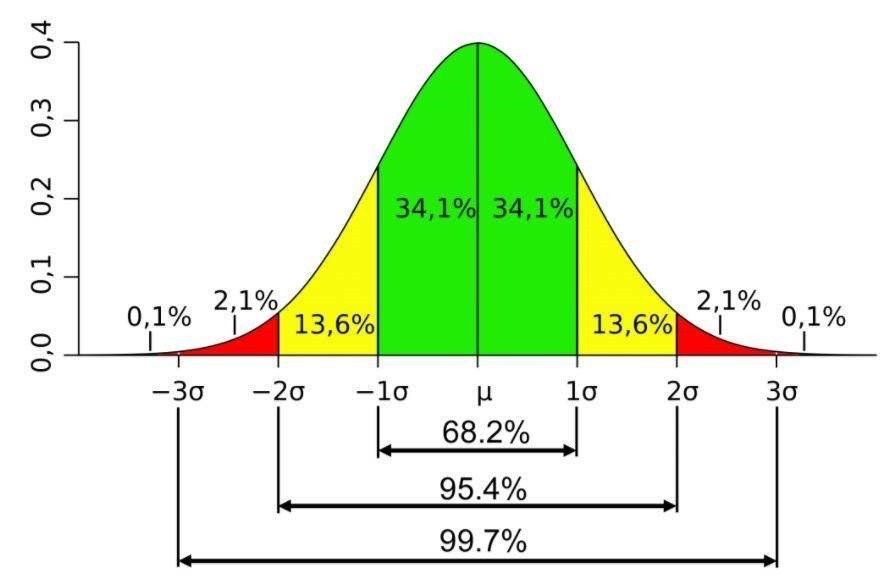
现在把前面算出的期望工期和标准差套入上图,就可以知道某个时间点完成的概率了。 先把期望工期21放到正中间的位置,然后把 期望工期 – 标准差 放到-1的位置,再把 期望工期 + 标准差 放到+1的位置。那么-1个标准差就是16, +1个标准差就是22。这个就叫正负一个标准差,概率为68.26%。
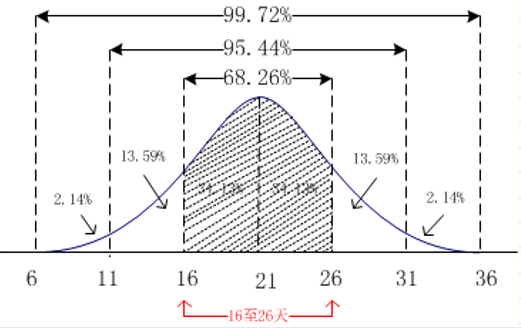
根据计算,一个标准差单位为5天,时间给定的范围16至26天,刚好距离我们所测算出来的均值21天的距离为正负一个标准差,所以在这个时间段内完成的概率为68.26%。
2)如问题为在26天完工的概率,则而16-26在+1的地方,是±1个标准差的一半,那么完成的概率就是34.13%。
根据0-21天完工概率+21-26天完工概率 =》 50%+68.26/2%=84.13%
