通过分析项目过程中哪个活动序列进度安排的总时差最少来预测项目工期的网络分析。
产生目的:为了解决,在庞大而复杂的项目中,如何合理而有效地组织人力、物力和财力,使之在有限资源下以最短的时间和最低的成本费用下完成整个项目。
关键路径是相对的,也可以是变化的。
关键路径可以有多条,关键路径上的活动时差为0。
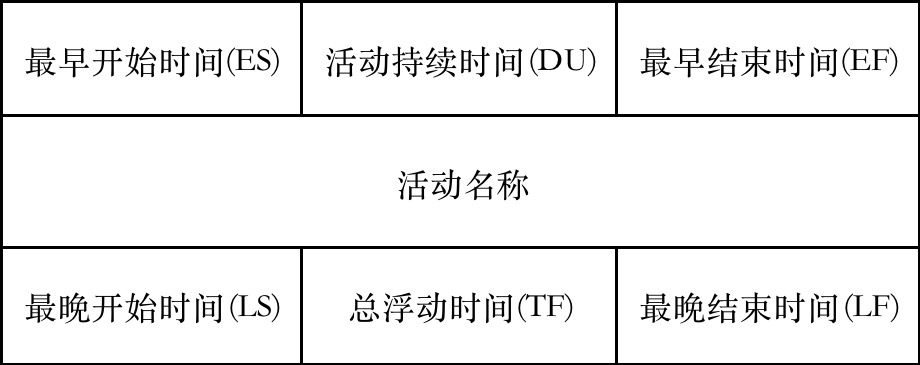
ES:最早开始时间(Earliest Start),是指某项活动能够开始的最早时间,只决定于项目计划,只要计划的条件满足了就可以开始的时间。
EF:最早结束时间(Earliest Finish),是指某项活动能够完成的最早时间。其中EF = ES+DU, DU为活动持续时间,顺推法先知道开始时间。
LF:最迟结束时间(Latest Finish),是指为了使项目在要求完工时间内完成,某项活动必须完成的最迟时间。往往决定于相关方(客户或管理层)的限制。
LS:最迟开始时间(Latest Start),是指为了使项目在要求完工时间内完成,某项活动必须开始的最迟时间。其中LS = LF -DU,DU为持续时间,逆推法先知道结束时间。
顺推法:
1、任一活动的最早开始时间,等于所有前置活动的最早结束时间的最大者;
2、任一活动的最早结束时间,等于该活动的最早开始时间 + 该活动工期 ;
3、 没有前置活动的,ES等于项目的开始时间。
EF = ES + DU
逆推法:
从网络图右侧开始,为每项活动制定最迟开始和最迟 结束时间,进行到网络图开始(最左边)。
1、任一活动的最迟结束时间,等于所有后续活动的最迟开始时间的最小者;
2、任一活动的最迟开始时间,等于该活动的最迟结束时间 – 该活动工期 ;
3、 没有后续活动的,LF等于项目的结束时间或者规定的时间。
LS = LF – DU
总浮动时间:
TF = LF – EF 或者 LS- ES ,活动在TF之间推迟不影响总工期(注意如果超 出该TF,则关键路径将发生变化),TF为0的路径为CP(关键路径)自由时差FF = 紧后ES – EF,活动在FF内推迟不影响紧后活动。
例子:
为了方便计算,以下例子以活动从第0天开始
(活动从第0天开始显然对人工计算来说更加直观简便,这种方法的缺点是与日历日期的对应关系是不一致的。活动从第1天开始计算的结果与日历日期是一致的,但是计算过程是不直观的。好在考试中一般不会涉及具体的日历日期,所以推荐使用活动从第0天开始的计算方法。)
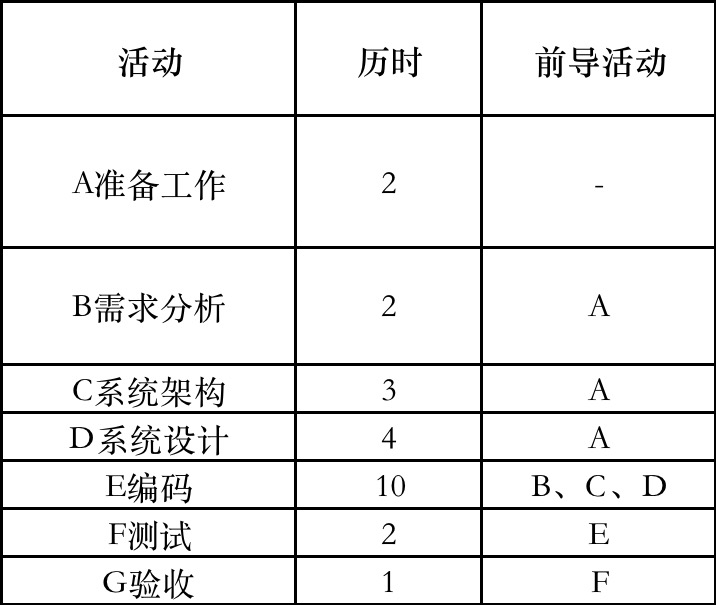
根据上面表格,我们可以通过顺推公式 EF = ES + DU 得到以下信息
顺推法 从左至右,取大值来 求ES和EF
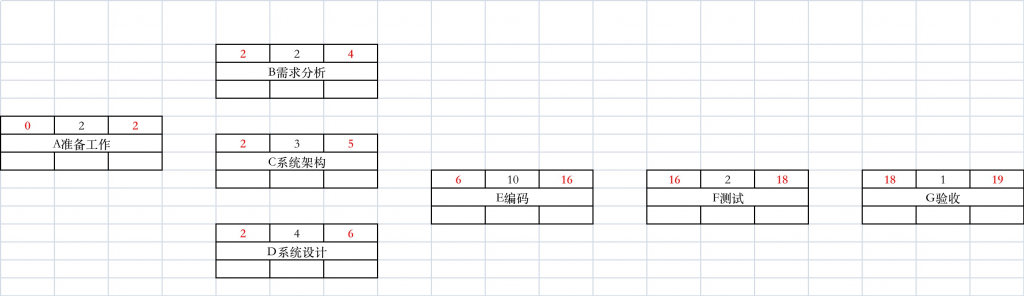
通过逆推公式 LS= LF – DU 得到以下信息
顺推法 从右至左,取小值来 求LS和LF
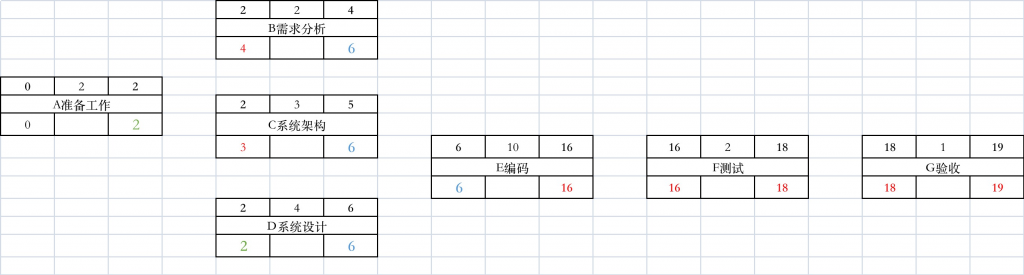
总浮动时间 TF = LF – EF
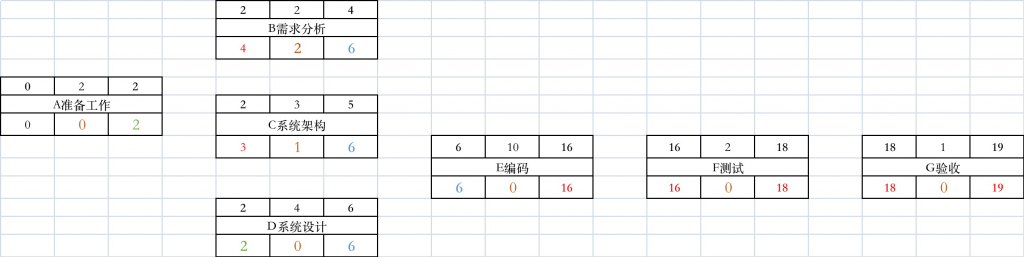
把所有总浮动时间为0的路径提取出来,则为关键路径 A-D-E-F-G
